Mapa de Karnaugh

Resumo

Mapas de Karnaugh, ou K-maps:
- são utilizados para simplificar expressões booleanas
- contém exatamente as mesmas informações que tabelas-verdade
- permitem que o processo de simplificação seja feito visualmente
- tornam-se inviáveis de serem representados a partir de 5 variáveis

1. Mapa de Karnaugh

O mapa de Karnaugh é uma representação visual de uma expressão booleana apresentado em 1953 por Maurice Karnaugh. O mapa de Karnaugh possui exatamente as mesmas informações que a tabela-verdade, entretanto, reduz a complexidade desta e representa a dada expressão booleana na forma de um mapa. O processo de simplificação, descrito na seção anterior utilizando álgebra de Boole, agora pode ser executado visualmente.

O mapa de Karnaugh é organizado de forma que, sempre que possível, produtos de termos logicamente adjacentes também sejam adjacentes na matriz, para serem logicamente combinados e, então, simplificados.

Produtos de termos são conjunções de variáveis (A and B) e dois produtos de termos são logicamente adjacentes quando eles contém as mesmas variáveis e diferem na forma de exatamente uma variável. Por exemplo, AB e AB’ são logicamente adjacentes, pois entre esses dois produtos de termos, somente a forma de B mudou (B para B’). Já AB e A’B’ não são logicamente adjacentes, uma vez que entre os dois produtos de termos, houve duas mudanças: de A para A’ e B para B’, quando somente uma variável pode mudar para que eles sejam logicamente adjacentes.

Cada célula do mapa de Karnaugh corresponde a uma linha na tabela-verdade e, consequentemente, também corresponde a um produto de termos fundamental.

Dessa forma, a tabela-verdade da porta AND, mostrada na Tabela 1, pode ser representada como o mapa de Karnaugh apresentado na Tabela 2.

Tabela 1. Tabela-verdade da porta AND.

A	B	A.B
0	0	0
0	1	0
1	0	0
1	1	1

Tabela 2. Mapa de Karnaugh para uma porta AND de duas entradas.

Z	A=0	A=1
B=0	0	0
B=1	0	1

Note que, se uma célula tem 1, então a expressão Z contém o produto fundamental indicado pela coluna e linha. Na Tabela 2, Y = 1 quando A = 1 e B = 1.

Podemos usar uma forma alternativa para indexar o mapa de Karnaugh, que é substituindo A = 1 por A e A = 0 por A’ nas colunas e B e B’ nas linhas, obtendo a Tabela 3.

Tabela 3. Representação alternativa do mapa de Karnaugh para uma porta AND de duas entradas.

Z	A’	A
B’	0	0
B	0	1

1.1 Exercícios

Exercício 1. Faça a tabela-verdade e mapa de Karnaugh para $Z=\overline{A}.\overline{B}+A.B$ . Que função é essa?

Solução

Seja $Z=\overline{A}.\overline{B}+A.B$ .

A tabela-verdade para a função $Z$ é:

$A$	$B$	$\overline{A}.\overline{B}$	$A.B$	$Z$
0	0	1	0	1
0	1	0	0	0
1	0	0	0	0
1	1	0	1	1

E o mapa de Karnaugh é:

Z	A’	A
B’	1	0
B	0	1

A tabela-verdade e o mapa de Karnaugh mostrados são da função XNOR.

Exercício 2. Usando o mapa de Karnaugh, encontre a expressão que representa a função XOR.

Solução

O resultado da função XOR é 1 quando A e B são diferentes (AB’ e A’B ) e 0, caso contrário. Assim, temos o seguinte mapa de Karnaugh para essa função.

Z	A’	A
B’	0	1
B	1	0

Vemos que existem dois produtos de termos que compõem a função XOR: $A\overline{B}$ e $\overline{A}B$ . Logo, a expressão que representa a função XOR é o produto de termos $\overline{A}B+A\overline{B}$ .

Exercício 3. Faça o mapa de Karnaugh para a função OR de duas entradas.

Solução

Z	A’	A
B’	0	1
B	1	1

2. Simplificação usando mapa de Karnaugh

Usar o mapa de Karnaugh de duas variáveis serve para ilustrar o processo de simplificação, que consiste de combinar produtos de termos fundamentais que são logicamente adjacentes. Vejamos exemplos de simplificação usando o mapa de Karnaugh.

Faça o mapa de Karnaugh para $Z=A\overline{B}+AB$ e use-o para obter a expressão simplificada.

Antes de fazer o mapa de Karnaugh, vamos usar as leis da álgebra de Boole que vimos para simplificar a expressão e ver onde iremos chegar, aplicando a propriedade da distributividade, temos:

$Z=A\overline{B}+AB$

$Z=A(\overline{B}+B)$

$Z=A$

O mapa de Karnaugh para $Z=A\overline{B}+AB$ é mostrado na Tabela 4.

Tabela 4. Mapa de Karnaugh para a expressão $Z=A\overline{B}+AB$

Z	A’	A
B’	0	1
B	0	1

Vemos que os dois produtos de termos fundamentais ( $A\overline{B}$ e $AB$ ) são logicamente adjacentes (estão na mesma coluna e diferem em uma variável) e, assim, sabemos que eles podem ser combinados.

Sabemos que a variável B será eliminada porque os termos adjacentes diferem nessa variável (um tem $\overline{B}$ e outro $B$ ), indicando que a expressão não depende do valor de B, enquanto ambos os termos possuem A. Dessa forma, a expressão é simplificada para Y = A.

O processo de simplificação é auxiliado visualmente pelo mapa de Karnaugh, mas pode também ser alcançado usando álgebra booleana, nem sempre de forma tão simples.

Exercícios

Use o mapa de Karnaugh para simplificar $Z=\overline{A}.\overline{B}+A.\overline{B}$ .

Solução

Temos uma soma de produtos de termos que pode ser facilmente ser representada em um mapa de Karnaugh da seguinte forma: a célula do mapa de Karnaugh indexada pela coluna $\overline{A}$ e linha $\overline{B}$ (correspondente ao produto de termos $\overline{A}.\overline{B}$ ) terá valor 1, assim como a célula correspondente ao produto de termos $A.\overline{B}$ .

Assim, temos:

Z	A’	A
B’	1	1
B	0	0

Os produtos $\overline{A}.\overline{B}$ e $A.\overline{B}$ são logicamente adjacentes e podem ser combinados. A variável $A$ é eliminada, porque os termos adjacentes diferem nesta variável, restando $\overline{B}$ .

Assim, a simplificação de $Z=\overline{A}.\overline{B}+A.\overline{B}$ é $Z=\overline{B}$ .

Use o mapa de Karnaugh para simplificar $Z=A\overline{B}+\overline{A}B + AB$ . Que função é essa?

Solução

O mapa de Karnaugh para a função é o seguinte:

Z	A’	A
B’	0	1
B	1	1

Os produtos de termos $A\overline{B}$ e $AB$ são adjacentes e podem ser simplificados para $A$ . O mesmo vale para os produtos de termos $\overline{A}B$ e $AB$ , que podem ser simplificados para $B$ . Logo, a expressão resultante é $A\overline{B}$ e $Z=A+B$ e a função representada pela expressão $A\overline{B}$ e $Z$ é a função OR.

3. Mapa de Karnaugh para mais de 2 variáveis

Dado que tabelas-verdade e mapas de Karnaugh contém exatamente a mesma informação, então um mapa de Karnaugh para n variáveis deverá conter 2ⁿ células. Na prática mapas de Karnaugh tornam-se inviáveis para mais que cinco variáveis (32 células).

Um mapa de três variáveis terá oito células e um exemplo é mostrado na Tabela 5.

Tabela 5. Mapa de Karnaugh para três variáveis. Cada célula mostra o produto de termos composto pela junção do índice da coluna e linha.

Z	$\overline{A}\overline{B}$	$\overline{A}B$	$AB$	$A\overline{B}$
$\overline{C}$	$\overline{A}\overline{B}\overline{C}$	$\overline{A}B\overline{C}$	$AB\overline{C}$	$A\overline{B}\overline{C}$
$C$	$\overline{A}\overline{B}C$	$\overline{A}BC$	$ABC$	$A\overline{B}C$

Vejamos alguns exemplos do uso do mapa de Karnaugh para 3 variáveis para simplificação de expressões.

3.1. Exercícios

Exercício 1. Faça a tabela-verdade e o mapa de Karnaugh para a função $Z=AB+\overline{A}C$

Solução

Temos a seguinte tabela-verdade para a função:

A	B	C	Z
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

A expressão tem três variáveis e o mapa de Karnaugh deve conter oito células. As variáveis A e B rotulam as quatro colunas no mapa (com as quatro combinações possíveis dessas duas variáveis, listadas de forma que sejam logicamente adjacentes: $\overline{A}.\overline{B}$ , $A\overline{B}$ , $AB$ e $\overline{A}B$ ) e a terceira variável, C, rotula as duas linhas: $\overline{C}$ e $C$ , como mostrado a seguir.

As informações da tabela-verdade são, então, passadas para o mapa. Por exemplo, na tabela-verdade, para A = 0, B = 0 e C = 1 o resultado de Z = 1. Logo, no mapa de Karnaugh, a célula indexada por $\overline{A}.\overline{B}$ e $C$ é 1 (pois $\overline{A}=0$ , $\overline{B} = 0$ e $C = 1$ ).

Temos, então, o seguinte mapa de Karnaugh:

$Z$	$\overline{A}.\overline{B}$	$\overline{A}B$	$AB$	$A\overline{B}$
$\overline{C}$	0	0	1	0
$C$	1	1	1	0

Exercício 2. Faça o mapa de Karnaugh para a função $Z=\overline{A}B\overline{C}+AC$ .

O mapa para a expressão é mostrado a seguir.

$Z$	$\overline{A}.\overline{B}$	$\overline{A}B$	$AB$	$A\overline{B}$
$\overline{C}$	0	1	0	0
$C$	0	0	1	1

O termo $\overline{A}B\overline{C}$ não pode mais ser combinado com nenhum outro produto de termos, então a expressão já está no formato mais simplificado.

Exercício 3. Faça o mapa de Karnaugh para a função $Z=\overline{A}.\overline{B}.\overline{C}+A.\overline{B}.\overline{C}$ e use para simplificar a expressão.

À primeira vista, parece que não há produtos de termos fundamentais que possam ser agrupados no mapa de Karnaugh a seguir.

$Z$	$\overline{A}.\overline{B}$	$\overline{A}B$	$AB$	$A\overline{B}$
$\overline{C}$	1	0	0	1
$C$	0	0	0	0

Enquanto em um mapa de duas variáveis todos os produtos logicamente adjacentes estão fisicamente ao lado um do outro, esse não é o caso para mais de duas variáveis.

Para um mapa de três variáveis, apesar de $\overline{A}.\overline{B}$ e $A\overline{B}$ serem logicamente adjacentes, eles não estão próximos fisicamente no mapa de Karnaugh, uma vez que estão na primeira e na última colunas.

Entretanto, eles estão conectados como se o mapa estivesse enrolado formando um cilindro, conectando as colunas 1 e 4, como mostrado na figura a seguir. Assim, os termos podem ser agrupados para formar $Z=\overline{B}.\overline{C}$

Mapa de Karnaugh

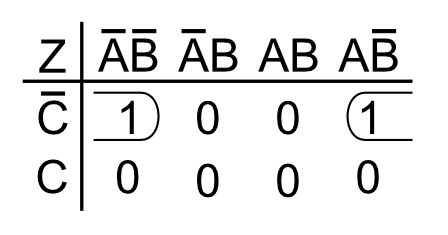
4. Exercícios

Exercício 1. Use o mapa de Karnaugh para encontrar a forma simplificada das seguintes expressões:

AB + AB’
AB + A’B + A’B’
AB’ + A’B’
ABC + ABC’ + AB’C
ABC’ + AB’C + AB’C’ + A’BC + A’BC’ + A’B’C
ABC + ABC’ + A’BC + A’B’C
ABC + ABC’ + AB’C + AB’C’ + A’B’C
ABCD + ABC’D + ABCD’ + A’BCD + A’B’CD + A’BCD’
ABC’D + AB’CD + AB’C’D + A’BCD + A’BC’D + A’BCD’ + A’B’C’D’
AB’C’D + AB’CD’ + AB’C’D’ + A’B’CD + A’B’C’D + A’B’CD’ + A’B’C’D’

Exercício 2. Como podemos usar a tabela verdade e mapa de Karnaugh para simplificar a expressão $Y=\overline{A.B} + \overline{A + B}$ ?

4. Referências

CROWE, John; HAYES-GILL, Barrie. Introduction to digital electronics. Elsevier, 1998.
LINCOLN, Betty. Introduction to Digital Electronics, 1/e. Pearson Education India, 2014.