1. Introdução

A álgebra de um sistema numérico descreve como executar operações aritméticas usando os operadores daquele sistema sobre as variáveis, que podem receber quaisquer valores dentro daquele sistema. A álgebra booleana é o sistema matemático que opera sobre dígitos binários (ou bits), mais especificamente 0s e 1s. Os circuitos digitais com uma ou mais entradas e uma saída capazes de executar operações lógicas são chamados de portas lógicas - as mais comuns são AND, OR e NOT.

Essas portas possuem dígitos binários como entradas e saídas e existe uma forma tabular para representar as saídas de uma porta dadas todas as entradas possíveis. Essa forma tabular é chamada de tabela-verdade.

1.1. Porta AND

A porta AND também é chamada de multiplicação lógica. Todas as combinações de duas entradas e saídas para a porta AND estão espresentadas na Tabela 1.

A expressão booleana para a porta (ou operação) AND aplicada aos operandos A e B é representada como:

Z = A.B, Z = AB, ou ainda , onde (.) e () representam a multiplicação lógica.

Tabela 1. Tabela verdade da porta lógica AND aplicada a duas entradas A e B.

A	B	A.B
0	0	0
0	1	0
1	0	0
1	1	1

O símbolo padrão da porta AND é mostrado na Figura 1.

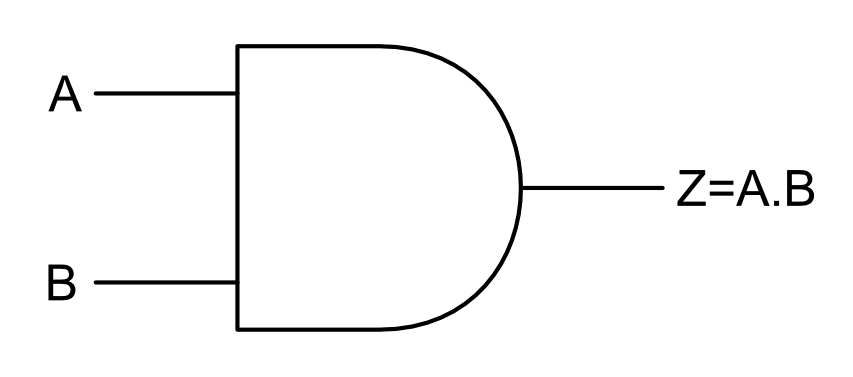Figura 1. O símbolo da porta AND.

1.2. Porta OR

A porta OR também é chamada de adição lógica. Todas as combinações de duas entradas e saídas para a porta OR estão espresentadas na Tabela 2.

A expressão booleana para a porta (ou operação) OR aplicada aos operandos A e B é representada como:

Z = A+B ou ainda , onde (+) e () representam a adição lógica.

Tabela 2. Tabela verdade da porta lógica OR aplicada a duas entradas A e B.

A	B	A+B
0	0	0
0	1	1
1	0	1
1	1	1

O símbolo padrão da porta OR é mostrado na Figura 2.

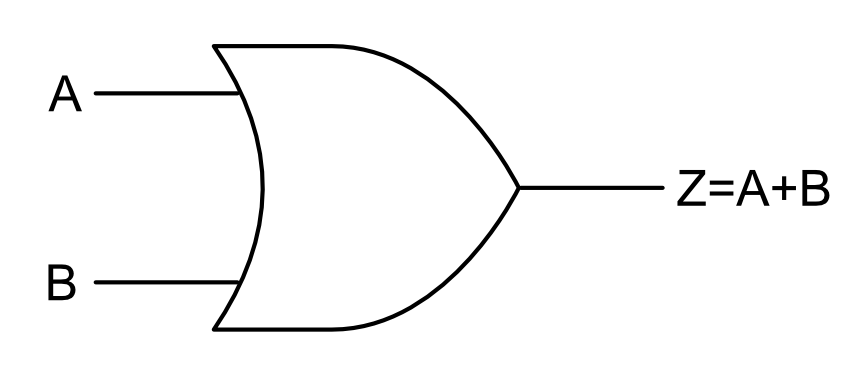Figura 2. O símbolo da porta OR.

1.3. Porta NOT

Uma variável booleana possui dois possíveis valores: 0 ou 1. O complemento de 0 é 1 e vice-versa. A porta NOT, também conhecida como inversor, produz o complemento de uma variável. Dessa forma, se A é a entrada de uma porta NOT, sua saída é representada por Z = ‘A ou , ou ainda .

A porta NOT possui somente um terminal de entrada, diferentemente das portas OR e AND, que possuem mais de uma entrada. A tabela-verdade da porta NOT é mostrada na Tabela 3.

Tabela 3. Tabela verdade da porta lógica NOT.

A	‘A
0	1
1	0

O símbolo padrão da porta NOT é mostrado na Figura 3.

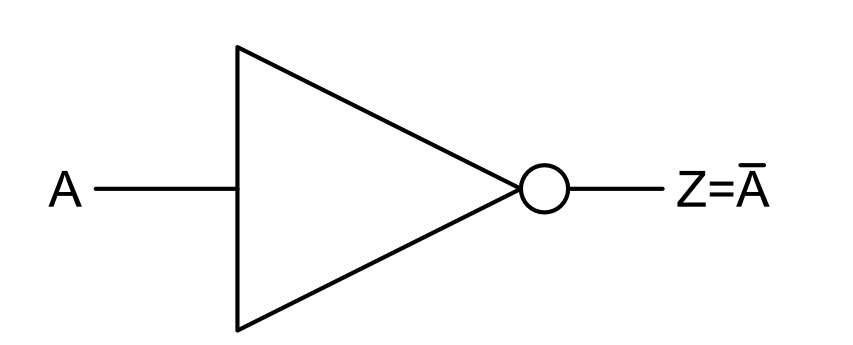Figura 3. O símbolo da porta OR.

1.4. Porta XOR (OU exclusivo)

Há, ainda, a porta OU exclusivo, abreviada como XOR, que tem duas entradas e uma saída. O símbolo padrão para a porta XOR é mostrado na Figura 4.

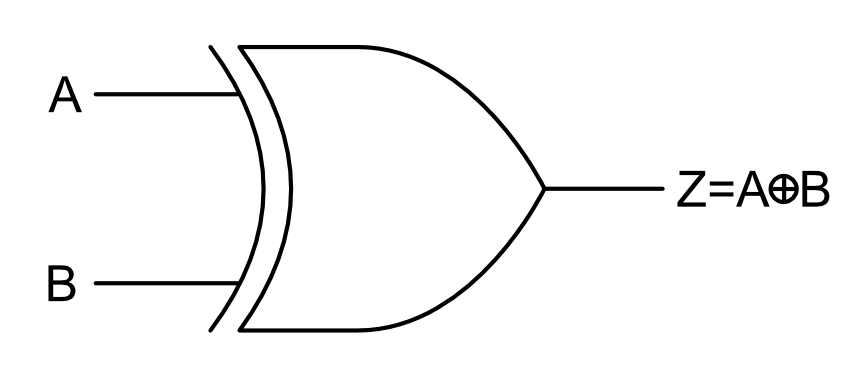Figura 3. O símbolo da porta XOR.

A saída da operação XOR é 1 quando as entradas são diferentes (A = 0 e B = 1 ou A = 1 e B = 0) ou 0 quando as entradas são iguais (A = 0 e B = 0 ou A = 1 e B = 1).

2. Exercícios

1. Represente as identidades booleanas a seguir usando portas lógicas básicas:
   1. Y = A⋅(B+C) + (E+F)⋅D
   2. Y = (A + B) ⋅ (C + D)
2. Usando a tabela verdade, mostre que: .
3. Implemente a expressão Y = AB + CD usando somente portas NAND.

3. Referências

1. CROWE, John; HAYES-GILL, Barrie. Introduction to digital electronics. Elsevier, 1998.
2. LINCOLN, Betty. Introduction to Digital Electronics, 1/e. Pearson Education India, 2014.