1. Conversões entre sistemas de numeração
1.1. Conversão de Binário para Decimal
Como já foi dito, o sistema binário, assim como o decimal, é um sistema de numeração posicional. Vamos, primeiramente, ver como isso funciona no sistema decimal, antes de passarmos para o binário. Considere o valor 7492. Em suas respectivas posições, os algarismos possuem os valores mostrados a seguir:
| Posição | 1000 | 100 | 10 | 1 |
|---|---|---|---|---|
| Algarismo | 7 | 4 | 9 | 2 |
| Valor | 7000 | 400 | 90 | 2 |
Para compor o valor total, multiplicamos os algorismos pelos valores das posições correspondentes: milhares (1000), centenas (100), dezenas (10) e unidades (1): 7 × 1000 + 4 × 100 + 9 × 10 + 2 × 1, que totaliza 7492. Perceba que, começando da posição mais à direita (1), os valores das próximas posições são o valor anterior * 10. Esse processo é natural para nós, que o realizamos sem nos dar conta.
Agora considere o valor binário 101102 (Usa se o 2 subscrito — 2 — para indicar que aquele valor é de base 2. A mesma coisa acontece para a base decimal — 10 — ou outras que estudaremos adiante).
Podemos construir a mesma tabela para descobrir o valor decimal correspondente a esse número binário. Entretanto, na tabela para binário, os valores das posições, a partir da 1, são o valor anterior * 2.
| Posição | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| Algarismo | 1 | 0 | 1 | 1 | 0 |
| Valor | 16 | 0 | 4 | 2 | 0 |
Para compor o valor total, multiplicamos os algarismos pelos valores das posições correspondentes: 16, 8, 4, 2 e 1: 1 × 16 + 0 × 8 + 1 × 4 + 1 × 2 + 1 × 1, que totaliza 22.
Veja mais exemplos a seguir:
11010012
| Posição | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| Algarismo | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| Valor | 64 | 32 | 0 | 8 | 0 | 0 | 1 |
Logo, o resultado é 1 × 64 + 1 × 32 + 0 × 16 + 1 × 8 + 0 × 4 + 0 × 2 + 1 × 1 = 105.
10011112
| Posição | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| Algarismo | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| Valor | 64 | 0 | 0 | 8 | 4 | 2 | 1 |
Logo, o resultado é 1 × 64 + 0 × 32 + 0 × 16 + 1 × 8 + 1 × 4 + 1 × 2 + 1 × 1 = 79.
1.2. Conversão de Decimal para Binário
Para converter da base 10 (decimal) para a base 2 (binário), utiliza-se o método das divisões consecutivas. Divide-se o valor decimal consecutivamente por 2 até que o resultado da divisão seja 1 e não seja mais possível continuar dividindo. Depois, a partir do resultado da última divisão, que será 1, utiliza-se os valores dos restos, de trás pra frente como é mostrado na Figura 4 (veja a seta vermelha)
Veja, a seguir, como funciona o método das divisões consecutivas na conversão do valor 158 para binário. O resultado é 10011110
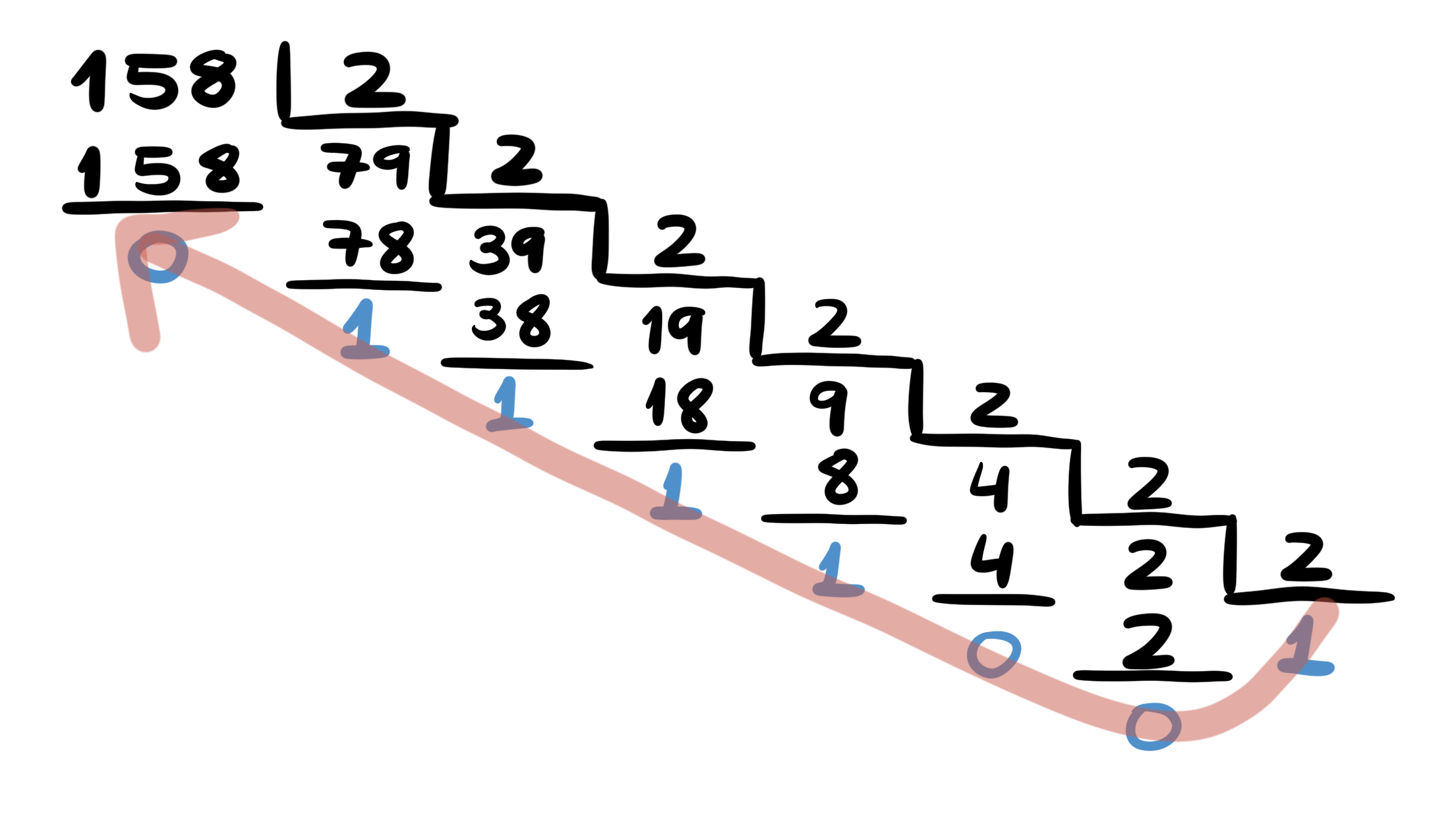Figura 4. Conversão do valor decimal 158 para binário.
1.3. Sistema de numeração octal
A conversão de octal para os outros sistemas de numeração pode ser feita usando os seguintes métodos:
- Para binário: transforme cada dígito octal em um agrupamento de 3 bits.
- Para decimal: atribua valores às posições de cada dígito–80 ao dígito menos significativo, 81 ao próximo dígito menos significativo, e assim por diante. Por fim, multiplique cada valor de posição por cada dígito e some todos.
- Para hexadecimal: converta para uma base intermediária antes de converter para hexadecimal.
1.4. Sistema de numeração hexadecimal
A conversão de hexadecimal para os outros sistemas de numeração pode ser feita usando os seguintes métodos:
- Para binário: transforme cada dígito hexadecimal em um agrupamento de 4 bits.
- Para octal: converta para uma base intermediária antes de converter para octal.- Para decimal: atribua valores às posições de cada dígito–160 ao dígito menos significativo, 161 ao próximo dígito menos significativo, e assim por diante. Por fim, multiplique cada valor de posição por cada dígito e some todos.
1.5. Material extra
Eu compilei nesse resumo as formas de conversão entre os sistemas de numeração binário, octal, decimal e hexadecimal.
Eu também preparei esse vídeo, demonstrando as conversões entre os quatro sistemas de numeração estudados.